デジタル概論　構成編　進数計算と論理回路　0から楽しむパソコン講座

１．2進数の負数(補数)・小数　

2進数の負数・少数の表し方はちょっと違います。 　

　前回の章では2進数について学んできました。２進数は０と１でしか表せません。
では、１０進数でマイナスの場合は２進数ではどうなるの？また、１０進数での小数点以下のの場合はどうなるの？といった疑問があると思います。当然、２進数は０と１（ONとOFF）しかありませんので、符号や小数点といったことは出来ません。と言いたいところですが、１０進数でのマイナス（負数）や小数点の場合の２進数の表し方があります。
ここでは、負数(補数）・小数の表し方について説明していきます。

1.１．2進数の負数（補数）について

まず「補数」という言葉をご存じでしょうか？
みなさんがよく利用しているwikipedia（ウィキペディア）では

「補数（ほすう;complement）とは、ある基数法において、ある自然数 a に足したとき桁が1つ上がる（桁が1つ増える）数のうち最も小さい数をいう。」

となっています。例えば１０進数で５５の補数は、桁の繰り上げは１００なので、
１００−５５＝４５
で補数は４５になります。

この補数を使って、１０進数の引き算を計算する場合、、例として８−７を計算してみましょう。
８−７　は　８＋（−７）ですよね。
ここで補数を使って計算する場合、１つルールを設けます。桁上がりした数字は無視てください。
７の補数は１０−７ですので、３です。
補数を使って計算すると、
８＋３＝１１ですが、先ほどの桁上がりした数字は無視するルールにすると、答は「１」です。

ちょっとややこしいですが、２進数の内部ではこの方法で計算を行っています。

２進数で負の数を表現する時は、先ほどの補数の技術を使います。
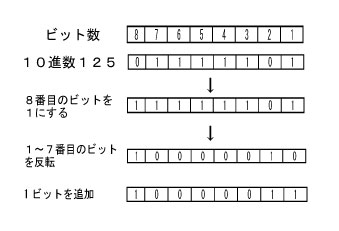
２進数の負数（補数の求め方は一番頭のビットを１にし、すべてのビットを反転させ１ビットを追加します。
例えば、１０進数で１２５を2進数に変換すると、０１１１１１０１となります。
１０進数で−１２５を表現する場合、まずは頭を１ビットにして、すべてのビットを反転させますので１０００００１０となります。それに１ビット追加するので、
答えは１０００００１１となります。

　なぜ、負数はこんな厄介な表わし方になるのかというのには理由があります。
中央演算装置は電気信号で行っているため、「引き算」が出来ません。引き算も「足し算」で行っています。なぜ「引き算」ができないかというのは後の「論理演算」の章で詳しく説明いたします。

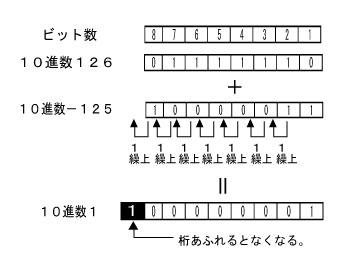
普通１２６−１２５＝１と簡単に求めることが出来そうですが、中央演算装置の内部では１２６＋（−１２５）というように変換し、足し算で「引き算」を行っています。

１０進数で１２６は進数では０１１１１１１０です。１２６−１２５を行う場合、中央演算装置内では０１１１１１１１０＋１０００００１１としています。その答えが０００００００１となります。

２．2進数の小数について

　10進数の整数を2進数に変換する方法は前章で説明しました。今回は10進数の小数を２進数に変換する方法を説明します。
10進数の小数部分を2進数に変換する場合は小数部分に2を掛け、整数部分が1の場合は2進数で「1」整数部分が0の場合は「0」にします。そして、整数部分を取り除き、小数部分だけ再度2を掛けて繰り返します。
例えば10進数で「0.625」を計算します。

0.625×2＝1.25　整数部分は「1」なので、2進数の小数部分の最初のビットは「1」です。
1.25の小数部分は0.25ですので、
0.25Ｘ2＝0.5　整数部分は「0」なので、2進数の小数部分の２つ目のビットは「0」です。
0.5Ｘ2＝1.0　整数部分は「1」なので、2進数の小数部分の３つ目のビットは「1」です。

よって0.625は2進数で0.101となります。

同じようにして10進数の「0.4」の2進数を求めてみましょう。

0.4×2＝0.8　整数部分は「0」なので、2進数の小数部分の最初のビットは「0」です。
0.8Ｘ2＝1.6　整数部分は「1」なので、2進数の小数部分の２つ目のビットは「1」です。
0.6Ｘ2＝1.2　整数部分は「1」なので、2進数の小数部分の３つ目のビットは「1」です。
0.2Ｘ2＝0.4　整数部分は「0」なので、2進数の小数部分の４つ目のビットは「0」です。
0.4Ｘ2＝0.8　整数部分は「0」なので、2進数の小数部分の５つ目のビットは「0」です。
0.8Ｘ2＝1.6　整数部分は「1」なので、2進数の小数部分の６つ目のビットは「1」です。
0.6Ｘ2＝1.2　整数部分は「1」なので、2進数の小数部分の７つ目のビットは「1」です。
0.2Ｘ2＝0.4　整数部分は「0」なので、2進数の小数部分の８つ目のビットは「0」です。
0.4Ｘ2＝0.8　整数部分は「0」なので、2進数の小数部分の９つ目のビットは「0」です。

ちょっとここで疲れてきましたね。同じことを繰り返していて終わりがなくなってきました。
10進数で0.4の2進数は「0.0110011001100･････」となってしまいます。このような形式を「循環小数」といいます。
10進数の表記で循環小数でなくても、2進数の変換すると循環小数になるものもあります。この現象については、プログラム上でもよくある現象です。
例えばエクセルなどで「浮動小数点」の形式で小数の数値を保存した場合、再度開くと数値が変わっている場合があります。0.3で保存したのに、再度開くと「0.29999999」になっていたりします。
また、プログラムを作っているときに、変数を浮動小数点にして変数に「0.3」を代入すると、結果が「0.30000000000000004」と出たり、「0.2+0.1」の結果を代入すると「0.29999999999999999」となったりします。
では、なぜ「0.3」という数値を出しているのかというと、2進数を10進数に変換してから小数部分の丸め込みを行っており、「0.3」と出しています。
プログラムを作成する場合、小数点を計算する場合、「切り上げ」、「切り捨て」、「四捨五入」というルールを明確にしなければ誤差が出ますので注意してください。

2.論理演算の概要　

２進数の計算では重要な「論理演算」
デジタルの世界で計算を行うことを「演算」と言いますが、通常私たちが使用している「四則演算」（足す・引く・掛ける・割る）の他に、デジタルの世界で非常に重要になってくるのが「論理演算」です。
論理演算とは「ブール演算」とも呼ばれ、「真」と「偽」の演算になります。
「真」は「その値です」ということで、「偽」は「その値ではありません」ということですが、デジタルの世界では「真」を「1（ON）」、「偽」を「0（OFF）」で表します。この論理演算は２進数の世界と密接な関係にありますので、きちんと理解してください。
論理演算には論理積（AND）、論理和（OR）、否定（NOT）、否定論理積（NAND）、否定論理和（NOR）、排他的論理和（XOR)の6種類があります。

これから論理演算で用いる集合の領域を表した「ベン図」、入出力パターンを表した「真理値表」、式、論理回路も同時に記載していきますので覚えて下さい。

　1.論理積（AND)

論理積は日本語で「〜かつ〜」という意味です。「条件にどちらも当てはまる」ときに「真」を出力します。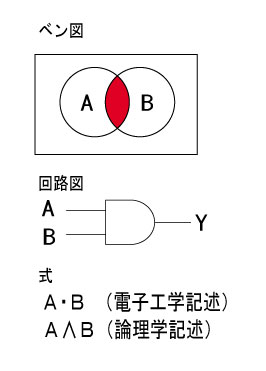

真偽値 入力A 入力B 出力Y 0 0 0 0 1 0 1 0 0 1 1 1

　2.論理和（OR)

論理和は日本語で「〜または〜」という意味です。「条件にどちらか当てはまる」ときに「真」を出力します。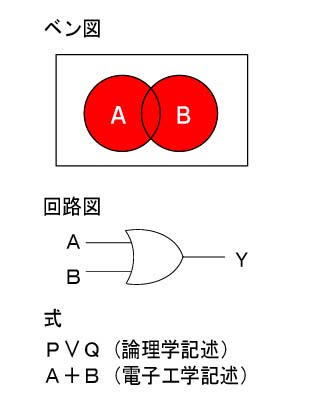

真偽値 入力A 入力B 出力Y 0 0 1 0 1 1 1 0 1 1 1 1

　3.否定（NOT)

否定は日本語で「〜でない」という意味です。「条件に当てはまらない」ときに「真」を出力します。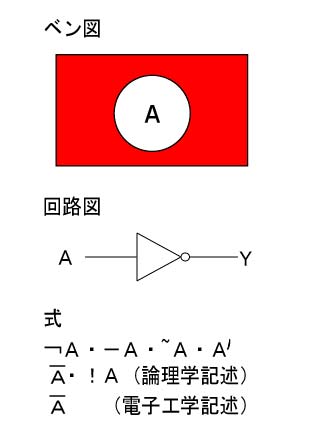

真偽値 入力A 出力Y 0 1 1 0

4.否定論理積（NAND）

　否定論理積は論理積（AND)を否定します。したがって「条件にどちらも当てはまることがない」ときに「真」を出力します。

真偽値 入力A 入力B 出力Y 0 0 1 0 1 1 1 0 1 1 1 0

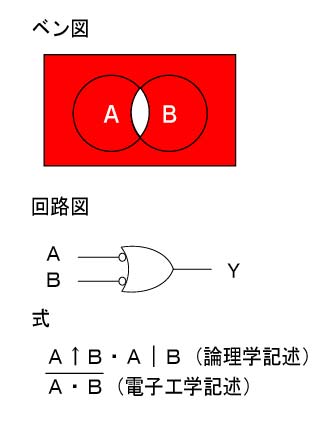　5.否定論理和（NOR）

否定論理和は論理和（OR)を否定します。したがって「条件にどちらか当てはまることがない」ときに「真」を出力します。

真偽値 入力A 入力B 出力Y 0 0 1 0 1 0 1 0 0 1 1 0

6.排他的論理和（NOR）

　排他的論理和は論理和（OR)の排他的な値のみが「真」となります。したがって両方の条件が当てはまるときは「偽」、片方の条件だけが当てはまるときだけ「真」を出力します。

真偽値 入力A 入力B 出力Y 0 0 0 0 1 1 1 0 1 1 1 0

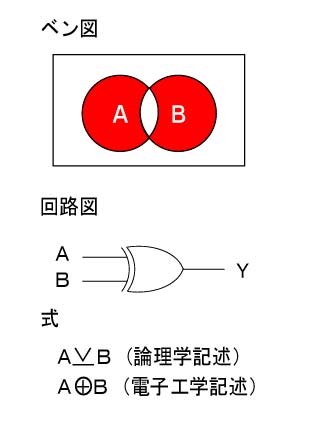これを使って、次章では実際に２進数の計算の仕組みを説明していきます。

　３．論理演算を使っての演算の仕組み　

　中央演算装置の計算は「回路」です。
中央演算装置は半導体で電気で動いているというのはご存知の通りですよね。電気はＯＮ・ＯＦＦしかありませんので、このＯＮ・ＯＦＦを使って計算しなければなりません。一体どうやって演算を行っているのでしょうか。電気のＯＮ・ＯＦＦの世界である２進数の加算を使って説明していきます。

　まずは、１桁目の位だけで考えていきます。

２進数の加算は
０＋０＝０
０＋１＝１
１＋０＝１
１＋１＝１０（下の桁０）

ですね。この法則、どこかで見かけませんでしたか？排他的論理和(XOR)の真偽値表と同じですよね。下の位は排他的論理和で計算を行っていることが分かります。
次に、桁上がりを考えましょう。

０＋０＝桁上がりなし（０）
０＋１＝桁上がりなし（０）
１＋０＝桁上がりなし（０）
１＋１＝桁上がりあり（１）

となります。この法則は論理積（AND)と同じ法則です。桁上がりの動作は論理積（AND)で行っています。

ビットA	ビットB	a＋bの値	上位への桁上がり
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1
A	B	AとBのXOR	AとBのAND

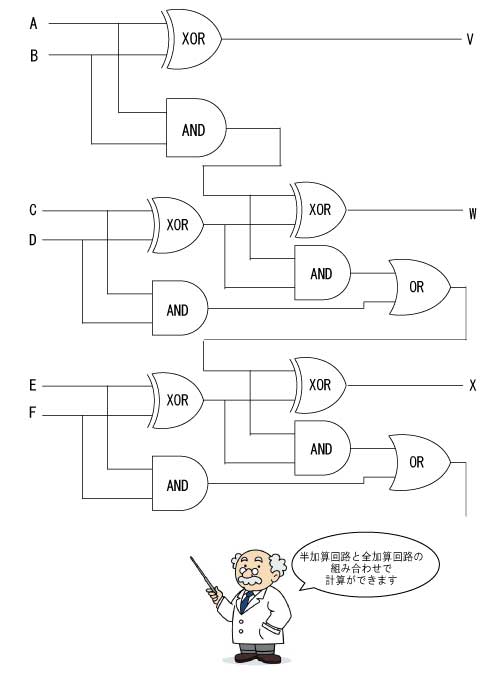
以上から、２進数の計算は排他的論理和(XOR)と論理積（AND)の合体で行っていることが分かりました。回路図は下図のようになります。




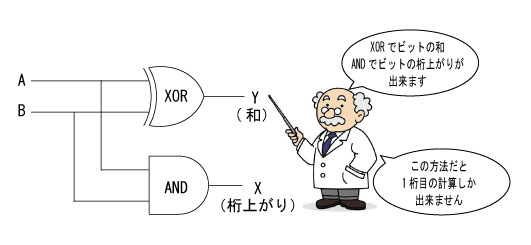
１桁目はいいけど、桁上がった２桁目の計算はどうすうるの？という疑問がふと生まれましたよね。上の回路は下の位からの桁上がりを無視した回路です。この回路を「半加算回路」といいます。
では、桁上がりを考慮した回路はどうなのでしょうか？
下の表から考えてみましょう。

ビットA	ビットB	下位からの桁上り値	a＋b＋cの値	上位への桁上がり
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

一見ややこしくなりますが、先ほどの「半加算回路」で下位の計算をXORで行っているということで、「ビットＡ」と「ビットＢ」の部分を論理演算の「XOR」に変えると下の表になります。

ビットAとBのXOR	下位からの桁上り値	a＋b＋cの値
0	0	0
0	1	1
1	0	1
1	1	0
1	0	1
1	1	0
0	0	0
0	1	1
A	B	AとBのXOR

上の表で「XOR」と「下位からの桁上がりの値」の演算結果が「a＋b＋cの値」として見た場合、ここも排他的論理和(XOR)になっているのに気付きましたか？排他的論理和(XOR)が2個使用していることが分かりました。
では桁上がりの部分はどうなっているのでしょうか？「半加算回路」では桁上がりは論理積（AND)で行っていると言いましたよね。
そこで、「ビットAとビットB」の論理積（AND)、「ビットAと下位からの桁上がり値」の論理積（AND)、「ビットBと下位からの桁上がり値」の論理積（AND)を作って見ましょう。
なぜこの３つの論理積を求めるかというと、パターンによって桁上がりが異なるため、この３つのパターンをまず作って見てください。そうすると下の表になります。

ビットAとBのAND	ビットAと桁上がりのAND	ビットBと桁上がりのAND	上位への桁上がり
0	0	0	0
0	0	0	0
0	0	0	0
0	0	1	1
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	1
A	B	C	AとBとCのOR

この３つの結果を論理和（OR)にすると、「上位の桁上がり」に一致しましたよね。これを回路図にすると下図のようになります。




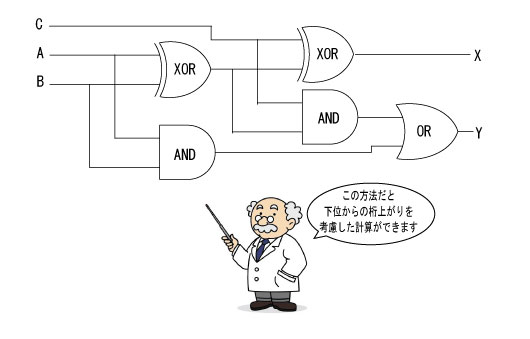
つまり、デジタルの世界では最初の１桁は「半加算回路」で、２桁目以降は「全加算回路」で計算を行っています。