デジタル概論　構成編　進数について　0から楽しむパソコン講座

1.進数（位取り記数法）とは　

数の数え方にはいろいろあります。進数を理解しましょう。 　

　私たちが普段数を数えるときに1.2.3.4.5.6.7.8.9.10と数えますよね。なんで1.2.3.4....と数えるの？と言うと、「小さいときに教えてもらった」「この数え方があたりまえでしょう」というでしょう。
それはその通り正解！！！です。　
しかし、身近な生活の場においてこの数え方が違うものがあります。
例えば、時間を数えるとき、６０秒になったら１分になります。６０分になったら１時間になります。２４時間になったら１日になります。これは当たり前ですよね、しかし、通常使用している10までの数え方の法則にはなっていません。６０分で繰り上げで単位が変わるというのは変ではないですか？

また鉛筆を数えるとき、１２本で１ダースと数えます。

このように、必ずしも普段の数え方の法則ではないのもあります。実際、この数え方は小さい時から教わって無意識のうちに使っているため、変に思わないでしょうが、通常の数え方とはちょっと違います。

私たちが通常1.2.3.4.5.6.7.8.9.10と使っている数え方は10進法と言います。一桁目が10個目に達した時位が上がり、一桁目がリセット（0になる）されます。
時間の場合、デジタル表記だと0〜59まで表記されるためちょっと分かりにくいですが、アナログ表記で見た場合、60秒や60分に針が来た場合、別の針が1個進み、元の針は0に戻ります。
そのため秒や分は60進数で行われており、同様に時間は24進数となります。
本来、古代の文明では時間の表記は60通りの文字があり、それを使って位を上げていたそうですが、現在は記載が非常にややこしくなるため、あえて10進表で表記しながら60進法を採用しています。

このように、「N」個目で位が上がり、下の位がリセットされる数え方を「N」進数と言います。

▲数の数え方にもいろいろあろます。

2.情報機器の内部は２進数　

なぜ情報機器は２進数の世界？
通常、私たちが使用している数え方は先ほども述べたとおり１０進数です。
しかし情報機器の内部は２進数で動いています。ではなぜ、２進数なのでしょうか？
２進数は電気や中央演算装置と密接な関係にあります。
ここでは２進数に関係する「単位」を使って情報機器が２進数を使用している理由を説明いたします。

　1.ビット（Bit)について

ビット（Bit)というのは、中央演算装置（CPU）で１つの電気のON・OFFを出来る回路を示します。
このビット（Bit）はほとんどのデジタルコンピュータが扱うデータの最小単位となり、後の章でも詳しく説明しますが、２進数での１桁となります。
情報機器の基盤には多数のIC（集積回路）が使われています。中央演算装置（CPU)も集積回路の一種です。集積回路は電気で動きますが、電気の世界では前に説明した通り「ON」と「OFF」の世界しかありません。そのため電気の「ON」の状態を２進数で「1」、「OFF」の状態を「0」で表しています。
電気には「電圧」というのがあるじゃないかと言う人もいると思いますが、集積回路には正確に電圧を認知できる機能がありません。また、電圧というのたえず変化しますから、電圧が変わった場合は間違ったデータになる可能性があります。そのため、確実にデータを転送するために電気の「ON」・「OFF」を使用しているわけです。
CPUで「32Bit（ビット）」や「64Bit（ビット）」という表記がありますが、1ビットは集積回路の１本の足で１つの「ON」・「OFF」の回路になります。ですから、32BitCPUは「ON」・「OFF」の回路が32個あるということになります。

　2.バイト(byte)について

1ビットは集積回路の１つの足で表せる１桁の単位というのは上記で分かったと思いますが、この1ビットを8桁まとめた単位を「Byte（バイト）」と言います。
本来、「バイト」は、欧文の１文字を表すためのビット数でありますが、昔はバイトの統一性がなく、「9ビット＝1バイト」や「6ビット＝1バイト」というコンピュータがありました。
しかし、IBM System/360という大型汎用機が多く市場に出回り、また1980年台に8ビットCPUを使用したマイクロコンピュータが爆発的に売れたこともあり、現在ではこの「8ビット＝1バイト」というのが規格になりました。
「バイト」という単位は主に記憶容量に用いられますが、記憶容量が100バイトとした場合、情報量として欧文文字で「100文字」保存できることを表します。

　3.ワード（Word)について

上記のビットやバイトという単位の他に、２進数ではワード（Word)という単位が使われます。
このワード（Word)という単位は使用する場面において、単位の定義が変わってきます。
ワードの単位の定義は３種類あります。

1.CPUの処理での単位（OSの定める標準サイズ）

　１ワードは中央演算装置（CPU）が一回で処理できる単位のことを言います。32ビットCPUの場合、32ビット＝4バイト（32÷8）＝1ワードになり、64BitビットCPUだと64ビット＝8バイト（64÷8）＝1ワードとなります。

2.「2バイト」

　その通り2バイト＝1ワードです。この単位はよく文字などの「コード体系」に使われます。

3.1つのアドレスのデータ量

　具体的なバイト数はまちまちになります。これはプログラムとも関係してきますが、作成するプログラムが1アドレスが何ビットなのかによって決まります。
WindowsのVisual C++の場合、1アドレスが1ビットで扱えるため、1ワード＝1ビットになります。

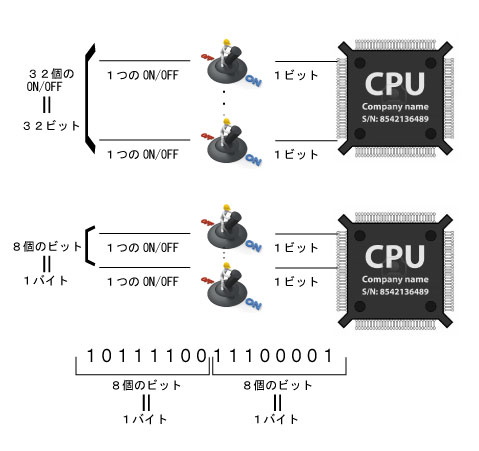▲ビット（Bit)・バイト（Byte）の説明図　ビットは１つのON・OFFの回路です。

　3.２進数を簡単に８進数・１６進数　

　２進数の計算は難しくありません。
デジタル機器の中で使用されている２進数。
私たちが使用している１０進数と２進数の変換は難しいように思われますが、数の数え方の方法の違いだけで、基本は一緒です。
２進数の世界はデジタル機器の世界に直結する反面、これを表記した時はとてつもない桁数を使用します。このため、これを簡略化するために「８進数」や「１６進数」といった数え方に変換します。
なぜ、「８進数」や「１６進数」に変換するのかというと、８や１６は２の乗数であり、２進数からの変換が容易であるためです。
それでは２進数・８進数・１０進数・１６進数への相互変換の方法を説明いたしましょう。

　１０進数と２進数の相互変換

　まずは８進数、１６進数を覚える前に、10進数を２進数に変換する計算方法を説明いたしましょう。
10進数を2進数に変換する場合は２で割り算を行い、余りを求めます。

たとえば10進数で３５の場合、

３５÷２＝１７あまり１
１７÷２＝８　あまり１
８　÷２＝４　あまり０
４　÷２＝２　あまり０
２　÷２＝１　あまり０
１　÷２＝０　あまり１

この余りを最初に割った余りから順番に並べます（右から左へ）
結果、３５の２進数は１０００１１となります。

２進数から１０進数に変換する場合、１が立っている桁を２の（桁−１）乗を掛けてやり、全部足していきます。

たとえば２進数で１１０００１の場合、

２の（６−１）乗＋２の（５−１）乗＋２の（１−１）乗＝３２＋１６＋１＝４９

となります。
小さい位から　１、１の２倍２、２の２倍４、４の２倍８、８の２倍１６、１６の２倍３２、３２の２倍６４．．．と覚えたほうが簡単かもしれません。

下の表は２進数と１０進数の相互表になります。

10進数	2進数		10進数	2進数		10進数	2進数		10進数	2進数
1	1		21	10101		41	101001		61	111101
2	10		22	10110		42	101010		62	111110
3	11		23	10111		43	101011		63	111111
4	100		24	11000		44	101100		64	1000000
5	101		25	11001		45	101101		65	1000001
6	110		26	11010		46	101110		66	1000010
7	111		27	11011		47	101111		67	1000011
8	1000		28	11100		48	110000		68	1000100
9	1001		29	11101		49	110001		69	1000101
10	1010		30	11110		50	110010		70	1000110
11	1011		31	11111		51	110011		71	1000111
12	1100		32	100000		52	110100		72	1001000
13	1101		33	100001		53	110101		73	1001001
14	1110		34	100010		54	110110		74	1001010
15	1111		35	100011		55	110111		75	1001011
16	10000		36	100100		56	111000		76	1001100
17	10001		37	100101		57	111001		77	1001101
18	10010		38	100110		58	111010		78	1001110
19	10011		39	100111		59	111011		79	1001111
20	10100		40	101000		60	111100		80	1010000

　２進数と８進数の相互変換

　
情報機器の内部ではこのように２進数が使われていますが、２進数を扱う場合桁数が多いため情報の記載が面倒になります。そのため、２進数を８進数や１６進数に変換して記載することがあります。
８進数の場合、３ビットごとに１つのブロックにします。２進数１１０の場合は８進数で６となります。（１０進数の変換と同じ考えです。）
２進数で１１０１１１の場合、１１０と１１１で分けます。１１０は６、１１１は７となりますので、２進数１１０１１１＝８進数６７となります

　２進数と１６進数の相互変換

　
１６進数の場合、４ビットごとに１つのブロックで分けて同様に計算しますが、１０進数で１０になった場合、１６進数では「Ａ」と表記します。１１だと「Ｂ」というように、１、２．．９、Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆとなります。

２進数で１１１０と場合、１０進数では１４となりますが、１６進数の場合は「Ｅ」となります。
２進数で１１０１１０１１の場合１１０１＝１０進数１３＝１６進数Ｄ、１０１１は１０進数１１＝１６進数Ｂとなるため１１０１１０１１＝１６進数「ＤＢ」となります。

下の表は１０進数・２進数・８進数・１６進数の相互表です。

10進数	2進数	8進数	16進数
1	1	01	1
2	10	02	2
3	11	03	3
4	100	04	4
5	101	05	5
6	110	06	6
7	111	07	7
8	1000	010	8
9	1001	011	9
10	1010	012	A
11	1011	013	B
12	1100	014	C
13	1101	015	D
14	1110	016	E
15	1111	017	F

２進数、８進数、１０進数、１６進数の表記方法

　２進数、８進数、１０進数、１６進数を区別するための表記があります。これはプログラムなどで進数表記が混在する場合によく使われます。

２進数の場合、末尾に「b」を付けて「1001b」と表記します。
８進数の場合、頭に「0（数字のゼロ）と付けて「052」と表記します
１０進数の場合、末尾に「d」を付けて｢95d｣と表記します。
１６進数の場合は、頭に「0x」を付けて「0xFF00」と表記したり、末尾に「h」を付けて「FF00h」と表記します。


なぜ8進数の頭に0を付けるのか

8進数を表記するとき、頭に「0」を付けて表記しますが、「まぎわらしい」「なぜ頭に0？」と思いませんか？
この謎を解くには、まずなぜ「8進数」を使用していたという所から始まります。
昔のコンピュータのＣＰＵの処理のビット数は現在の「４の倍数」ではなく「３の倍数」でした。そのため12ビットや15ビット機なども数多く存在していました。
そのため昔は16ビットではなく８ビットが主流だったわけです。
プログラム上で8進数と16進数の区別を付けるために「Octal」の頭の１文字を取って「Ｏ（オー）」を付けるという案が出ました。しかし、頭に「Ｏ（オー）」が出た場合、その次は英字か数字か分かりません。先頭が「Ｏ（オー）」の単語はいくつもあります。
そこで「Ｏ（オー）」に似た「0（ゼロ）」を頭に付けよう。しかも10進数では普通は頭に「0（ゼロ）がつかないため一石二鳥となり、現在の頭に「0（ゼロ）を付けたと言われています。

最後の進数変換器を載せますので試してみてください。

進　数　変　換　機
10進数の値を、2進数から16進数までの値に変換します。
変換される値 例　123456	進　数 例　16		結　果 例　1e240